| Главная | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Предварительно напряженные комбинированные стержневые и вантовые конструкции3.2. Расчет гибких нитей и предварительно напряженных стержневых конструкций методом конечных элементов Плоские и пространственные предварительно напряженные конструкции, однопоясные и двухпоясные висячие системы, плоские и объемные пространственные сети могут быть рассчитаны при едином подходе методом конечных элементов. Начало развития этого метода было заложено в шестидесятые и семидесятые годы, получило в последствии широкое применение при расчете различных конструкций. Использование этого метода позволяет производить как статические, так и динамические расчеты, применяя единый алгоритм подготовки и ввода исходных данных для конструкций различного вида и уровня сложности. Существенный вклад в развитие метода конечных элементов внесли как отечественные ученые [13], [15], [31], так и зарубежные специалисты, позволившие разработать целый ряд универсальных программ для расчета на ЭВМ. К ним относятся ЛИРА, ГАММА, Mikrofe и другие отечественных авторов, а также NASTRAN, OKABUS, ANSYS, FLOWERS и другие зарубежных разработчиков. Несмотря на очевидные преимущества, применение метода конечных элементов имеет и определенные недостатки. Использование метода упрощается в тех случаях, когда
С другой стороны, при проведении расчетов могут возникнуть некоторые трудности, которые преодолеваются с помощью специальных приемов. К таким проблемам относятся:
3.2.1. Теоретические основы метода конечных элементов для расчета предварительно напряженных стержневых и вантовых систем В расчете таких конструкций методом конечных элементов принимаются следующие предпосылки:
188
Эти предпосылки значительно упрощают расчет и позволяют рассматривать канатные конструкции как стержневые системы. При этом необходимо учитывать, что вантовые конструкции отличаются от стержневых тем, что первые из них могут быть многократно статически неопределимыми и при определенных условиях геометрически изменяемыми. 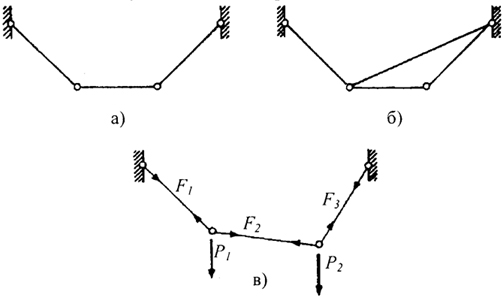 Рис. 3.11. Геометрическая изменяемость отдельных систем: а - система геометрически изменяема; б, в - системы геометрически неизменяемые. На рис. 3.11, а показана простая канатная система, являющаяся геометрически изменяемой. Для схем рис. 3.11,6 и 3.11,в геометрическая неизменяемость обеспечена благодаря наличию достаточного количества стержней (рис. 3.11,6) или наличию внешней нагрузки. Такие системы являются нелинейными, для их решения используются различные итеративные методы. Наиболее распространенными из них являются методы Эйлера, Ньютона-Рафсона и другие. 3.2.1.1. Матрица жесткости шарнирно-опертого стержневого и канатного элементов При расчете вантовых и предварительно напряженных комбинированных конструкций производится учет деформируемого состояния при составлении уравнений равновесия. Рассмотрим элемент, деформирующийся в плоскости под действием узловых сил. Из геометрических соотношений, принимая начальную длину l = 1, можно получить (рис. 3.12) 189 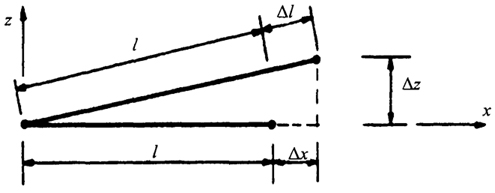 Рис. 3.12. Деформированное состояние стержня (3.44) Раскладывая в степенной ряд подкоренное выражение (3.44),получим: ε = u'x +
ε; =
(3.45 а) Для деформирования стержня в пространстве выражение (3.45 а) имеет вид: ε = u'x +
(3.45 б) В уравнениях (3.45 а) и (3.45 б) все слагаемые кроме первого являются нелинейными составляющими, зависят от деформированного состояния. Эти выражения применены в дальнейшем для определения энергии деформации стержневой системы, с помощью которой, используя первую теорему Кастелиано [103], находят матрицу жесткости для рассчитываемой конструкции. Выражение для энергии деформации U имеет вид: U =
или U =
(3.46) при A = const, где А, Е - площадь сечения и модуль упругости стержня (E = const); σ - напряжение в стержне. Подставляя значение деформаций (3.45 б) в (3.46), получим U =
(3.47) или 190 U = U(0) + U(1) + U(2)(3.48) где U(0) =
(3.49) U(1) =
(3.50) U(2) =
(3.51) Составляющие сил, приложенных к стержню Si, по направлениям действующих деформаций di могут быть получены с учетом теоремы Кастелиано из выражения Si =
(3.52) Коэффициенты матрицы жесткости выглядят следующим образом kij =
(3.53) Матрица жесткости элементов для расчетов с учетом геометрической нелинейности имеет вид К = К(0)+К(1)+К(2)(3.54) где К(0) - линейная составляющая матрицы жесткости; K(1), К(2) - нелинейные добавки, учитывающие деформированное состояние стержневой системы при загружении, причем для К(1) входящие параметры перемещения в первой степени и для К(2) - во второй. Соотношение между усилиями в узлах и перемещениями узлов для любого шарнирно-опертого элемента на ступени загружения q (рис. 3.13) в каждой системе координат (х, у, z) имеет в матричной форме следующий вид: К · δ = S(3.55) где δ = {d1d2d3d4d5d6} - вектор перемещения узлов в локальной системе координат. s = {S1S2S3S4S5S6} - вектор усилий в узлах. К = К(0)+К(1)+К(2) - тангенциальная матрица жесткости стержня в локальной системе координат. Составляющие тангенциальной матрицы жесткости шарнирно опертого элемента имеют следующий вид [50], [84]: 191 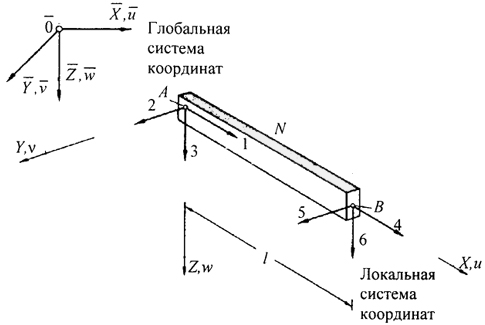 Рис. 3.13. Шарнирно опертый стержневой элемент: 1,2,3... - направления перемещений
(3.56) где К11 = К44 = -K41 = l K(1) =
(3.56)
192 K(2) =
(3.58)
Зависимость между узловой нагрузкой и перемещениями узлов в глобальной системе координат (X,Y,Z) имеет вид K · δ = S(3.58)
Переход от параметров матрицы жесткости, перемещений и усилий в локальной системе координат к соответствующим значениям в глобальной системе координат (рис. 3.14) осуществляется следующим образом К = Т · К · ТT(3.60) d = T · d(3.61) d = TT · d(3.62) S = TT · S(3.63) S = T · S(3.64) Здесь Т - матрица направляющих косинусов; ТT - транспонированная матрица Т; d, S - соответственно перемещения узлов и усилия в элементах в глобальной системе координат; d,S - перемещения узлов и усилия в элементах в локальной системе координат. Матрица направляющих косинусов может быть записана в виде: 193 T =
(3.65) где Cy =
Cy =
Cz =
l = √lx2 + ly2 + lz2 , l1 = √lx2 + lz2. 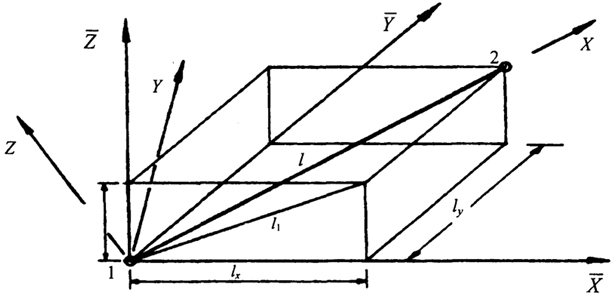 Рис. 3.14. Переход от локальной к глобальной системам координат 3.2.1.2. Матрица жесткости изгибаемого стержневого элемента Для изгибаемого элемента относительная деформация под нагрузкой может быть представлена в виде ε = u' +
(3.66) где z, у - соответственно координаты точки в сечении стержня относительно осей у и z. Подставляя значение (3.66) в выражение для энергии деформации можно получить матрицу жесткости (3.4) для изгибаемого элемента по направлениям перемещений согласно рис. 3.15. 194 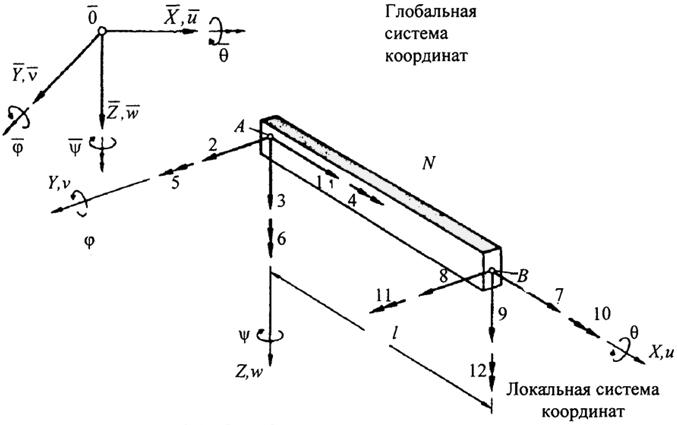 Рис. 3.15. Изгибаемый элемент в пространстве
(3.67) где K11 = K77 = -K71 =
K26 = K3,11 = -K8,12 = 6 ·
K35 = K3,11 = -K9,11 = -6 ·
K55 = K11,11 = 4 ·
K66 = K12,12 = 4 ·
195 Первая нелинейная компонента K1 =
(3.68) где K11 = K77 = -K71 = 3 · (d7 - d1); K21 = -K81 = -K72 = K87 =
K31 = -K91 = -K73 = K97 =
K51 = -K75 = -
K61 = -K76 =
K11,1 = -K11,7 = -
K12,1 = -K12,7 =
K22 = K33 = K88 = K99 = -K82 = -K93 =
K62 = K12,2 = -K53 = -K11,3 =
K95 = -K86 = -K12,8 = K11,9 =
K55 = K66 = K11,11 = K12,12 =
K11,5 = K12,5 =
Вторая нелинейная компонента 196 K2 =
(3.69) где K11 = f1 · [3 · (d7 - d1)2 +
K77 = -K71 = K11; K21 = f1 · [-2 · (d7 - d1) · (
K81 = K72 = -K21; K31 = f1 · [-2 · (d7 - d1) · (
K91 = K73 = -K31; K51 = f1 · [2 · (d7 - d1) · (
K75 = -K51; K61 = f1 · [2 · (d7 - d1) · (-
K76 = -K61; K11,1 = f1 · [2 · (d7 - d1) · (
K11,7 = -K11,1; K12,1 = f1 · [2 · (d7 - d1) · (-
K12,7 = -K12,1; 197 K22 = f2 · [864 · (d2 - d8)2 + 216 · l · (d2 - d8) · (d6 + d12) + 36 · l2 · (d62 + d122) + 168 · (d7 - d1)2] + f2 · [288 · (d3 - d9) · (d5 + d11) + 12 · l2 · (d52 + d112)]; K88 = K22; K32 = f2 · [576(d2 - d8) · (d3 - d9) - 72 · l · ((d2 - d8) · (d5 + d11) - (d3 - d9) · (d6 + d12)] - f2 · [24 · l2 · (d5 · d6 + d11 · d12)]; K92 = K83 = -K32; K52 = f2 · [-72 · l · (d2 - d8) · (d3 - d9) + 24 · l2 · (d5 · (d2 - d8) - d6 · (d3 - d9)] - f2 ·[2 · l3 · (d5 · (d6 - d12) - d11 · (d6 + d12))]; K63 = K85 = -K52; K62 = f2 · [108 · l · (d2 - d8)2 + 72 · l2 · d6 · (d2 - d8) - 3 · l2 · (d62 - 2 · d6 ·d12 - d122) + 28 · l · (d7 - d1)2] + f2 · [36 · l · (d3 - d9)2 - 24 · l2 ·d5 · (d3 - d9) - l3 · (d52 - 2 · d5 · d11 - d112)]; K86 = -K62; K11,2 = f2 · [-72 · l · (d2 - d8) · (d3 - d9) + 24 · l2 · (d11 · (d2 - d8) - d12 · (d3 - d9)] - f2 · [2 · l3 · (d11 · (d6 - d12) - d5 · (d6 + d12))]; K12,3 = K11,8 = -K11,2; K33 = f2 · [864 · (d3 - d9)2 - 216 · l · (d3d9) · (d5 + d11) + 36 · l2 · (d52 + d112) + 168 · (d7 - d1)2] + f2 · [288 · (d2 - d8)2 + 72 · l · (d2 - d8) · (d6 + d12) + 12 · l2 · (d62 + d122)]; K99 = -K93 = K33; K53 = f2 · [-108 · l · (d3 - d9)2 + 72 · l2 · d5 · (d3 - d9) + 3 · l3 · (d52 - 2 · d5 · d11 - d112)] - f2 · [28 · l · (d7 - d1)2 - 36 · l · (d2 - d8)2 - 24 · l2 · d6 · (d2 - d8) + l3 · (d62 - 2 · d6 · d12 - d122)]; K95 = -K53; K11,3 = f2 · [-108 · l · (d3 - d9)2 + 72 · l2 · d11 · (d3 - d9) + 3 · l3 · (d52 + 2 · d5 · d11 - d112)] - f2 · [28 · l · (d7 - d1)2 - 36 · l · (d2 - d8)2 - 24 · l2 · d12 · (d2 - d8) - l3 · (d62 + 2 · d6 · d12 - d122)]; K11,9 = -K11,3; K55 = f2 · [36 · l2 · (d3 - d9)2 + 6 · l3 · (d3 - d5) · (d5 - d11) + 12 · l4 · (2 · d52 -
198 K65 = f · [-24 · l2 · (d2 - d8) · (d3 - d9) - 2 · l3 · ((d5 - d11) · (d2 - d8) - (d6 - d12) · (d3 - d9)] + f · [16 · l4 · (d5 · d6 -
K11,5 = f2 · [-6 · l3 · (d3 - d9) · (d5 + d11) - 3 · l4 · (d52 -
K12,5 = f · [2 · l3 · ((d2 - d8) · (d5 + d11) - (d3 - d9) · (d6 + d12))] - f · [4 · l4 · (
K11,6 = K12,5; K66 = f2 · [36 · l2 · (d2 - d8) - 6 · l3 · (d2 - d8) · (d6 - d12) + 12 · l · (2 · d62 -
K12,6 = f2 · [6 · l3 · (d2 - d8) · (d6 + d12) - 3 · l4 · (d62 -
K11,11 = f · [36 · l2 · (d3 - d9)2 - 6 · l3 · (d3 - d9) · (d5 - d11) + 12 · l4 · (
K12,11 = f2 · [-24 · l2 · (d2 - d8) · (d3 - d9) + 2 · l3 · ((d2 - d8) · (d5 - d11) - (d3 - d9) · (d6 - d12))] + f2 · [16 · l4 · (
K12,12 = f2 · [36 · l2 ·(d2 - d8)2 + 6 · l3 · (d2 - d8) · (d6 - d12) + 12 · l4 · (
f1 =
199 Для изгибаемых элементов матрица направляющих косинусов имеет вид T12x12=
(3.70) где T1 =
(3.71) здесь l2 = √t12 + t22 + t32; l3 = √txy2 + tyz2 + txz2; txy =
tyz =
txz =
200 |