Начертательная геометрия. Способы преобразования ортогональных проекций.

§ 18. Понятие о коллинеарном
преобразовании пространства

Проективная геометрия, рассматривая пространство как совокупность точек, прямых и плоскостей, допускает возможность преобразования этого пространства в новое и устанавливает определенное соответствие, при котором точке А соответствует точка А₀; плоскости π,

73

проходящей через точку А, соответствует плоскость π₀; проходящей через точку А₀, прямой 1 соответствует прямая 1₀.

Такое соответствие в пространстве называют коллинеарным.

Если мы возьмем какую-либо фигуру Φ и преобразуем ее в новую фигуру Φ₀ так, чтобы каждой точке второй фигуры соответствовала определенная точка первой фигуры, то принято говорить, что фигура Φ₀ находится в коллинеарном соответствии с исходной фигурой Φ.

Преобразование, которое дает возможность придать исходной фигуре Φ свойства новой фигуры Φ₀, называется коллинеарным преобразованием.

Если считать, что фигура Φ неразрывно связана с пространством, в котором она расположена, то преобразование этой фигуры в новую Φ₀ можно рассматривать как результат деформации пространства.

Поэтому характер коллинеарного преобразования фигуры станет известным, если будут заданы условия, при которых исходное пространство может быть деформировано в новое (преобразованное) пространство.

Деформация трехмерного пространства вполне определяется, если будут даны пять произвольных, по четыре не лежащих в одной плоскости точек деформированного пространства, соответствующих пяти, также по четыре не лежащим в одной плоскости, точкам исходного пространства, т.е. в общем случае задания коллинеарного преобразования на чертеже мы должны показать пять произвольных точек исходного (первого) пространства и соответствующие им пять точек преобразованного (второго) пространства.

Следует подчеркнуть, что перемещение точек из первого пространства во второе в частном случае может происходить по прямым линиям, называемым линиями связи.

При этом величина перемещения для каждой точки может быть произвольной, отличной от величины перемещения других точек.

Можно представить случай, когда перемещение одной или нескольких точек будет равно нулю¹, т.е. исходное и преобразованное положение этих точек совпадают. Такие точки принято называть двойными. Очевидно, проведя через две двойные точки прямую или через три двойные точки плоскость, мы получим соответственно двойные прямую и плоскость, которые будут сами себе соответствовать при коллинеарном преобразовании пространства.

74

Рис. 72	Рис. 73

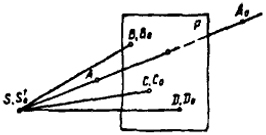
Гомологическое преобразование пространства. Гомологическим преобразованием пространства или просто гомологией называется такое преобразование, при котором из пяти точек, определяющих характер коллинеарного соответствия, четыре будут двойными, причем одна из них не должна лежать в плоскости трех других.

В общем случае гомология может быть задана: произвольной плоскостью (три двойные точки); одной точкой, не меняющей в процессе преобразования своего положения в пространстве (четвертая двойная точка); исходным и преобразованным положением пятой точки.

На рис. 72 показан общий случай задания гомологии в пространстве пятью точками ABCD и S, при этом точки BCD и S - двойные: три первые определяют плоскость Р, которую называют двойной плоскостью преобразования или плоскостью гомологии. Любые точки этой плоскости при преобразовании остаются самими собой.

Четвертая двойная точка S называется центром преобразования или центром гомологии.

Пятая точка показана в исходном А и преобразованном A₀ положении.

Отметим некоторые свойства гомологии.

1. Линии связи, соединяющие точки первого (исходного) пространства с точками второго (преобразованного) пространства, образуют связку прямых, проходящих через центр гомологии.
2. Каждой точке (прямой, плоскости) первого пространства соответствует точка (прямая, плоскость) второго пространства.
3. Прямая, не параллельная плоскости гомологии, пересекается с соответствующей ей прямой на двойной плоскости преобразования.
4. Плоскость, не параллельная плоскости гомологии, пересекается с соответствующей ей плоскостью по прямой, лежащей в двойной плоскости преобразования.

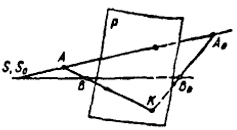
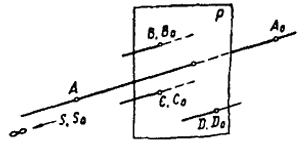
Если гомологическое преобразование задано, то не составляет труда определить положение любой точки пространства после ее преобразования.

75

На рис. 73 показаны построения, которые необходимо выполнить, чтобы найти точку B₀, если известно ее положение до преобразования (B).

Построения выполнены в следующем порядке:

Через точки A и В проводим прямую до пересечения ее с плоскостью Р в точке К. При преобразовании точка К остается неизменной, так как она принадлежит двойной плоскости; поэтому прямая АВ преобразуется в прямую А₀К.

Так как точка В принадлежит АВ, то в силу инциденции точки и прямой B₀ будет находиться на A₀K.

Для определения В₀ проводим линию связи SB до пересечения ее с А₀К.

Перспективно-аффинное (родственное) преобразование пространства. Значительный интерес, с точки зрения возможности использования в начертательной геометрии, представляет частный случай гомологического преобразования пространства, при котором центром гомологии является несобственная точка. В этом случае линии связи, по которым перемещаются точки пространства в процессе преобразования, окажутся параллельными между собой.

Преобразование, характерное единым направлением перемещения точек, называется перспективно-аффинным (или родственным), а соответствие, им установленное,- перспективно-аффинным (или родственным) соответствием.

Перспективно-аффинное преобразование вполне определяется четырьмя парами точек, из которых три двойные (задают плоскость преобразования).

Рис. 74 дает наглядное представление о способе задания перспективно-аффинного преобразования. Линия связи АА₀ указывает направление преобразования.

В данном случае двойная плоскость преобразования Р называется плоскостью родства.

При удалении в бесконечность центра преобразования свойства гомологии сохраняются. При этом первое свойство гомологии для случая перспективно-аффинного преобразования следует сформулировать так: линии связи, соединяющие точки первого пространства с соответствующими (в данном случае родственными) точками второго пространства, параллельны между собой.

Параллельность линий связи дает возможность, кроме уже перечисленных четырех свойств гомологии, для перспективно-аффинного преобразования отметить дополнительные свойства, которыми не обладает гомология:

76

Рис. 74	Рис. 75

• 1) параллельным прямым (плоскостям) первого пространства соответствуют родственные параллельные прямые (плоскости) второго пространства;
• 2) отношение отрезков прямой равно отношению отрезков родственной прямой;
• 3) плоскость, параллельная плоскости родства, параллельна родственной ей плоскости, а каждая фигура этой плоскости конгруентна родственной ей фигуре.

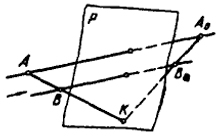
Если определен характер перспективно-аффинных преобразований, нахождение точек, родственных заданным, производится просто.

На рис. 75 показаны все построения, которые нужно выполнить, чтобы найти положение точки В₀, родственной заданной точке В при условии родства, определяемого плоскостью Р и положением точек А и А₀.

Построения выполнены в следующем порядке: через точки A и В проводим прямую до пересечения ее с плоскостью родства (точка К). Соединяем К с A₀, получаем прямую A₀K, родственную АК. Через точку В проводим прямую, параллельную АА₀ (направлению родства), до пересечения ее с А₀К в точке B₀.

В зависимости от направления аффинного преобразования пространство может подвергаться деформации сжатия, растяжения, сдвига, а также сочетания сдвига с растяжением или сжатием.

Приведенные выше чертежи дают нам наглядное представление; во-первых, о задании коллинеарного (гомологического или родственного) преобразования пространства (рис. 72,74); во-вторых, о характере графических построений, которые нужно выполнить, чтобы найти положение точек, соответствующих заданным (рис. 73, 75).

Решение задач в ортогональных проекциях осуществляется на эпюре. Естественно, практический интерес представляет такое задание коллинеарного преобразования, которое позволяет проще находить точки (фигуры), соответствующие заданным точкам (фигурам) непосредственно на эпюре.

Мы видели, что для нахождения точек, соответствующих (в данном коллинеарном соответствии) заданным, необходимо в качестве

77

Рис. 76	Рис. 77	Рис. 78

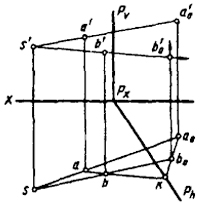
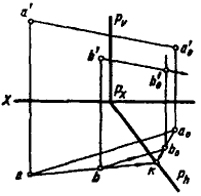
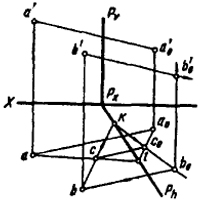
вспомогательных построений определять точки встречи прямых с двойной плоскостью. Очевидно, эти построения могут быть значительно сокращены, если двойную плоскость принимать проецирующей.

При этом наиболее экономичными (в смысле уменьшения количества графических построений) будут частные положения проецирующей плоскости, а именно положения, параллельные плоскости проекции.

При таком задании двойной плоскости ее след будет осью плоского коллинеарного соответствия (гомологического или родственного).

На рис. 76 показано построение В₀, соответствующей заданной точке В. Преобразование гомологическое задано плоскостью гомологии Р, центром S, исходным А и преобразованным А₀ положением точки А.

Плоскость гомологии выбрана горизонтально-проецирующей, поэтому горизонтальные проекции ее двойных точек совпадут с горизонтальным следом этой плоскости. Следовательно, P_h, является двойной прямой осью плоской гомологии и в сочетании с горизонтальными проекциями s, а и а₀ определит гомологию плоских полей. Эта плоская гомология представляет горизонтальную проекцию элементов, задающих гомологию пространства.

В этом случае решение гомологического преобразования пространства мы можем свести к гомологическому преобразованию плоских полей [9].

Для нахождения точки b₀ через точки а и b проводим прямую до пересечения ее с осью гомологии. Точку k соединяем с a₀, получаем соответствующую ak прямую a₀k. Так как до преобразования точка b находилась на прямой ak, то после преобразования она останется на соответствующей прямой a₀k. Прямая sb пересечет а₀k в искомой точке b₀. По b₀ определяем b'₀.

78

Для нахождения точки В₀ преобразованного пространства, состоящей в перспективно-аффинном соответствии с заданной точкой В исходного пространства, воспользуемся плоским коллинеарным соответствием.

Родственное преобразование задано плоскостью родства Р и парой родственных точек А и А₀ (рис. 77).

Положение точки b'₀ определяется, как и в предыдущем примере, с той лишь разницей, что проекции линии связи bb₀ и b'b'₀ будут параллельны одноименным проекциям направления преобразования, которое определяется родственными точками АА₀. Все построения ясны из чертежа и не требуют пояснений.

На рис. 78 представлен случай, когда точка пересечения прямой АВ с осью родства не находится в пределах чертежа. В этом случае для определения b₀ необходимо через а провести прямую (al), пересекающую ось родства. На этой прямой взять произвольную точку С и найти родственную ей точку С₀ (положение точки С на прямой AL выбираем так, чтобы прямая ВС пересекала ось родства в пределах чертежа).

Дальнейшие построения проводятся как в предыдущем примере.

Не будем останавливаться на рассмотрении всевозможных вариантов построения отрезков прямой, плоских фигур или многогранников, коллинеарно соответствующих заданным. При желании читатель сможет самостоятельно (пользуясь рис. 76-78) выполнить необходимые построения¹.

При дальнейшем изложении остановимся более подробно на пространственном преобразовании криволинейных поверхностей.

Рассмотрение этого вопроса начнем с частного случая гомологии - перспективно-аффинного преобразования.

79