| Главная | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Высшая математика. Том 1: Элементы линейной алгебры и аналитической геометрии§ 12. Векторное произведение 12.1. Два определения векторного произведения. Зададим в некоторой прямоугольной системе координат трехмерного действительного пространства векторы а = (аx, ау, аz), b = (bх, bу, bz) и назовем векторным произведением а и Ъ вектор 96
В качестве последнего члена этой цепи написан "обобщенный определитель", первая строка которого состоит из векторов i, j, k (ортов системы координат). Во втором члене показано, как этот обобщенный определитель понимать (определитель третьего порядка мы разлагаем по элементам первой строки так, как если бы i, j, k были числами). Очевидно, что [а ×(-b)] = -[а × b], Векторное произведение векторов а и b можно также определить следующим образом:
|c| = |а| |b|sin ω (0 < ω < π). (2) где ω есть угол между а и b, т. е. длина с равна площади параллелограмма, построенного на векторах а и b (рис. 29). Докажем эквивалентность сформулированных двух определений. Если вектор с = 0, то из (1) следует, что компоненты векторов а и Ь пропорциональны ах : ау : аz - bх : bу : bz 97
т. е. а и b коллинеарны, но тогда векторное произведение и по второму определению равно нулевому вектору. Обратно, если а и b коллинеарны, то по второму определению а × b = 0. Так как компоненты векторов а и Ь при этом пропорциональны, то, согласно первому определению, с - 0. Пусть теперь а и b - неколлинеарные векторы и с - их векторное произведение согласно (1). Очевидно, что (с, а) = (аybz - аzbу)ах + (аzbх - аxbz)ау + (аxbу - аybx)аz = 0 и аналогично (с, b) = 0. Итак, вектор с перпендикулярен к а и b. Докажем, что система векторов (а, b, с) ориентирована так же, как система координат х, у, z. Будем непрерывно вращать векторы а и b вокруг точки О, каждый раз вычисляя по ним вектор с, но так, чтобы все время а и b были неколлинеарными. Но тогда вектор с все время будет ненулевым (с ≠ 0) и система (a, b, с) все время будет некомпланарной. Совершим такие повороты, чтобы векторы а и b получили направления соответственно осей х и у, т. е. чтобы они имели вид а = (|а|, 0, 0), b = (0, |b|, 0). Этого всегда можно достигнуть, потому что в данном случае плоскость векторов а, b может вращаться в пространстве. Но тогда вектор с, вычисленный по формуле (1), имеет 98 вид с = (0, 0, |а| |b|). Мы видим, что векторы (а, b, с) в последний момент нашего процесса ориентированы так же, как оси (х, у, z). Но тогда, согласно определению ориентации (см. § 11) и исходная система а, b, с ориентирована так же, как система координат х, у, z. Итак, векторное произведение с = а × Нам еще надо доказать формулу (2). Пусть векторы а и b образуют с осями координат углы, соответственно равные α, β, γ, α’, β’, γ’. Так как
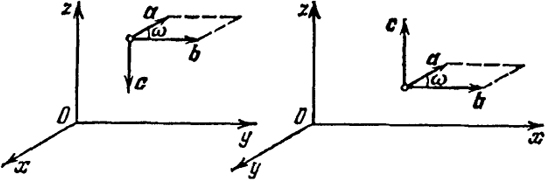
то 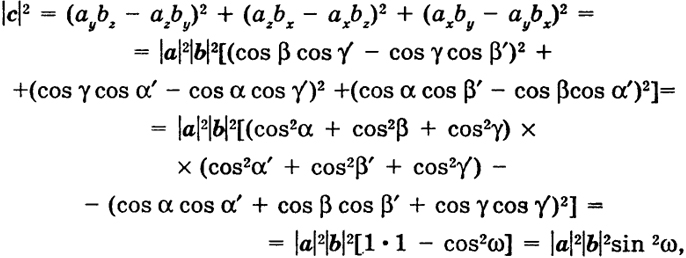 где ω - угол между векторами a и b (cos ω = cos α cos α’ + + cos β cos β’ + cos γ cos γ’). Итак, мы доказали (2). Таким образом, мы полностью доказали, что из определения векторного произведения по формуле (1) следует второе его определение. Обратно, если вектор подчиняется второму определению, тогда он единственный, потому что может быть только один вектор, перпендикулярный к а и Ь, длина которого равна площади параллелограмма, построенного на 99 а, b, и притом такой, что система (а, b, с) ориентирована так же, как система х, у, z. Но тогда это есть вектор с, определенный по формуле (1), потому что последний, как мы убедились, обладает указанными свойствами. Отметим еще раз, что условие а × b = 0 есть необходимое и достаточное условие коллинеарности векторов а и b. 12.2. Геометрический смысл определителя второго порядка. Рассмотрим теперь специально два ненулевых плоских вектора а = < (аx, аy), b = (bx, bу) (3) в некоторой прямоугольной системе координат х, у (рис. 30, 31). Будем считать, что рассматриваемая плоскость находится в пространстве и добавим к осям х, у
перпендикулярную к ним ось z. Векторы а, b будут теперь иметь координаты а = (ах, ау, 0), b = (bх, bу, 0). Векторное произведение их равно
100 где k - орт оси z. По определению векторного произведения система (а, b, с) ориентирована, как система координат х, у, z. Поэтому, очевидно, если определитель
то система векторов (а, b) должна быть ориентирована, как оси координат (х, у). Если же определитель
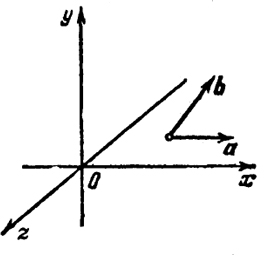
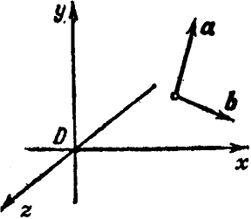
то система (а, b) ориентирована противоположно ориентации х, у. На рис. 30 изображена первая ситуация расположения векторов (a, b), a на рис. 31 - вторая. Мы знаем также, что площадь параллелограмма, построенного на векторах а и b, равна (см. (4))
т. е. абсолютной величине определителя
Итак, мы доказали, что: 1) абсолютная величина определителя (5) равна площади параллелограмма, построенного на векторах а = (ах, ау) и b = (bx, by); 2) знак определителя (5) зависит от расположения этих векторов относительно прямоугольной системы координат х, у. Знаку + соответствует система (а, b), ориентированная, как х, у, а знаку - соответствует система (а, b), ориентированная противоположным образом. 101 12.3. Свойства векторного произведения. Справедливы свойства а × b = -[b × a], (6) а × (αb) = α[а × b], (7) а × (b + с) = [а × b] + [а × с], (8) где а, b, с - произвольные векторы, α - скаляр. Если векторные произведения, входящие в равенства (6), (7), (8), выразить по формуле (1) через компоненты векторов а = (ах, ау, аz), b = (bx, bу, bz), с = (сх, су, сz). то легко получить эти равенства. Формулы (6) и (7) легко следуют также из геометрических соображений. Пусть а и b - неколлинеарные векторы. Если в векторном произведении заменить местами а и b, то площадь параллелограмма, построенного на а и b, и перпендикуляр к а и b не изменятся. Изменится лишь направление с = а × b на противоположное, что влечет изменение ориентации (а, b, а × b). Умножение на положительное число а вектора b увеличивает лишь в α раз площадь параллелограмма, построенного на а и b, а направление векторного произведения останется прежним. Если же а< 0, то а × (αb) = а × (-|а|b) = |а|[а × (-b)] = Заметим еще, что из (6) и (7) следует также, что (αa) × b = -[b × (αa)] = -α[b × а] = а[а × b]. Пример 1. Определить угол А треугольника ABC с вершинами А = (1, 2, 3), B = (2, 2, 2), С = (1, 2, 4). Обозначим искомый угол через ω. Таким образом, ω это угол между векторами
102 sin ω =
где
Отсюда sin ω =
Так как
Замечание. Если в треугольнике ABC угол А прямой, то |
Пример 2 (из механики). Пусть заданы две точки А и В. К точке В приложена сила, определенная вектором F. Пусть а =
b = а × F (см. рис. 32,
103 Вектор b (момент силы F) перпендикулярен к векторам а и F и имеет длину, равную площади параллелограмма, построенного на векторах а и F. Направление же вектора b зависит от той прямоугольной системы координат, которая задана в этом вопросе. На рис. 32 взята левая система координат. Направление b взято так, чтобы векторы a, F, b тоже образовали левую систему. 104 |
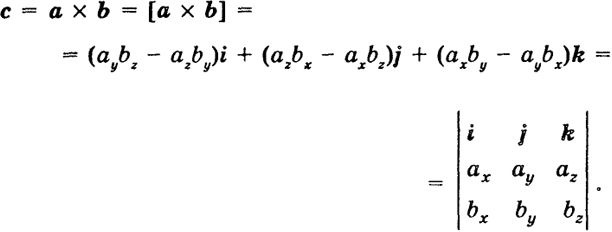 (1)
(1)
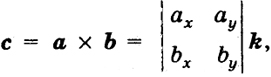 (4)
(4)
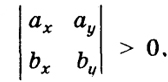
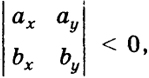

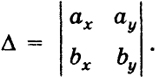 (5)
(5)