| Главная | |||||||||||||||||||||
Высшая математика. Том 1: Элементы линейной алгебры и аналитической геометрии§ 14. Линейно независимая система векторов Зададим в Rn (действительном или комплексном) систему из k векторов as = (as1, as2, …, asn) (s = 1, …, k) (1) По определению система (1) линейно независима, если из векторного равенства λ1a1 + λ2a2 + ... + λkak = 0, (2) 105 где λ1, λ2, ..., λk - числа (соответственно действительные или комплексные), следует, что λ1, = λ2 = ... = λk = 0. Система векторов (1) называется линейно зависимой, если существуют числа λ1, λ2, … , λk, одновременно не равные нулю, для которых выполняется равенство (2). Если для определенности считать, что λk ≠ 0, то из (2) следует, что аk = μ1a1 + ... + μk-1аk-1, (3) где μ1 = -
Таким образом, если система из k векторов линейно зависима, то один из них есть, как говорят, линейная комбинация остальных, или, как еще говорят, зависит от остальных. Так как все время будет идти речь о линейной зависимости, то термин линейный будем позволять себе иногда опускать. Будем также говорить зависимые или независимые векторы вместо зависимая или независимая система векторов. Один вектор а1 тоже образует систему - линейно независимую, если а1 ≠ 0, и зависимую, если а1 = 0. Если система векторов а1, ..., аk линейно независима, то любая часть этой системы а1, ..., as (s< k) тем более линейно независима. Иначе нашлась бы нетривиальная система чисел λ1, ..., λs, для которой выполнялось бы λ1а1 + ... + λsas = 0,
но тогда для системы λ1, ..., λs, λ1a1 + ... + λsas + 0 ∙ as+1 + ... + 0 ∙ аk = 0. 106 Из сказанного следует, что если система векторов а1, ..., аs линейно зависима, то любая пополненная система а1, . . . , аs, as+l, . . . , аk обладает тем же свойством. В частности, система векторов, содержащая в себе нулевой вектор, всегда линейно зависима. Составим матрицу, определяемую векторами системы (1): 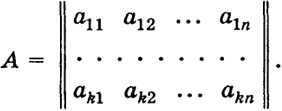 Теорема 1. Если ранг А = k, т. е. ранг А равен числу векторов, то система (1) линейно независима. Если же ранг А < k, то система (1) линейно зависима. Пример 1. Два вектора а1 = (а11, а12), а2 = (а21, а22) в действительном пространстве R2 образуют линейно независимую систему, если определитель
потому что векторное уравнение λ1а1 + λ2а2 = 0 (4) эквивалентно двум уравнениям для соответствующих компонент
Но если Δ ≠ 0, то система (5) имеет единственное тривиальное решение λ1 = λ2 (6) 107 Если же Δ = 0, то уравнениям (5) удовлетворяет некоторая нетривиальная система (λ1, λ2), т. е. при Δ = 0 система векторов а1, а2 линейно зависима. Очевидно, сказать, что в действительном пространстве R2 векторы а1 и а2 коллинеарны или линейно зависимы - это все равно. Но тогда сказать, что векторы а1 и а2 не коллинеарны или линейно независимы - это тоже все равно.
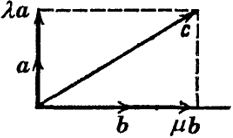
Пример 2. Система векторов а1, а2, ..., аk (k ≥ 3) в действительном пространстве R2 всегда линейно зависима. Геометрически это ясно из рис. 33: если с - произвольный вектор и a, b - неколлинеарные векторы, то всегда можно указать такие числа λ, μ, что с = λа + μb. Это показывает, что система а, b, с линейно зависима. Если же а и b - коллинеарные векторы, то они линейно зависимы. Тем более линейно зависимы а, b, с. По теореме 1, чтобы исследовать пару векторов a1, а2, мы должны записать матрицу из их координат
В данном случае k = 2.
Это совпадает с приведенными выводами, потому что в случае а) Δ = 0 и б) Δ ≠ 0. Тот факт, что три произвольных вектора а1, а2, a3 в R2 линейно зависимы, тоже предусмотрен теоремой - ведь ранг А ≤ 2 < 3 = k. 108 Пример 3. В трехмерном действительном пространстве R3 два вектора а1 = (а11, а12, а13), а2 = (а21, а22, а23) линейно зависимы тогда и только тогда, когда они коллинеарны. В самом деле, пусть а1, а2 коллинеарны. Если один из данных векторов нулевой, то они линейно зависимы. Если же а1 и а2 коллинеарны и не нулевые, то а1 = λа2, где λ - некоторое число. Последнее означает, что а1, а2 линейно зависимы. Обратно, если a1, а2 линейно зависимы, то один из них зависит от другого, например а2 = μа1, т. е. векторы коллинеарны. Если в этом случае рассмотреть матрицу
то элементы строк матрицы пропорциональны, и поэтому ранг А = 1 < 2 = k, т. е. наше утверждение согласуется с теоремой 1. Пример 4. Рассмотрим теперь три вектора в R3: а1 = (а11, а12, а13), Пусть
109 Векторному уравнению λ1a1 + λ2a2 + λ3а3 = 0 (7) эквивалентна система из трех уравнений
Если Δ ≠ 0, то система (7') имеет единственное тривиальное решение λ1 = λ2 = λ3 = 0. Но тогда и уравнение (7) имеет единственное тривиальное решение и система векторов а1, а2, а3 линейно независима. Если Δ = 0, то система (7'), следовательно, и уравнение (7) имеют нетривиальное решение (λ1, λ2, λ3). Но тогда система векторов (a1, а2, a3) линейно зависима. Но здесь можно различать детали: 1) Пусть ранг А = 1, где
Тогда по крайней мере одна из строк А, пусть для определенности первая, имеет хотя бы один элемент, не равный нулю. Рассмотрим матрицу
Она имеет ранг 1, поэтому все порождаемые ею определители второго порядка равны нулю
110 Но тогда, очевидно, компоненты векторов а1 и а2 пропорциональны
т. е. a21 = a11 λ, a22 = a12λ, a23 = a13λ или а2 = λа1 Аналогично, учитывая, что в матрице
тоже все определители второго порядка равны нулю, получим, что а3 = μa1, где μ - некоторое число. Таким образом, в этом случае векторы а1, а2, а3 коллинеарны. 2) Пусть теперь ранг А = 2. Тогда одна из матриц, состоящих из двух строк матрицы А, имеет ранг 2. Пусть для определенности это есть матрица А' (см. (8)). На основании примера 3 векторы а1 и а2 линейно независимы. Но система а1, а2, а3 зависима, т. е. для некоторой нетривиальной тройки чисел (λ1, λ2, λ3) λ1а1 + λ2а2 + λ3а3 = 0. (9) Здесь λ3 ≠ 0, потому что иначе λ1а1 + λ2а2 = 0, и в силу независимости системы а1, а2 было бы λ1 = λ2 = 0. Но тогда равенство (9) можно разрешить относительно а3: a3 = μ1a1 + μ2a2, μ1 = -
111 Таким образом, если Δ = 0, а ранг А' - 2 (см. (8)), то векторы а1 и а2 неколлинеарны, а вектор а3 принадлежит к плоскости этих векторов. Приведенные рассуждения не противоречат теореме 1. В самом деле, если Δ ≠ 0, то ранг А = 3 = k и по теореме 1 система векторов a1, а2, а3 линейно независима. Если же Δ = 0, то ранг А< 3 и система векторов а1, а2, а3 линейно зависима. Доказательство теоремы 1. Векторное равенство (2) эквивалентно следующим п уравнениям для компонент векторов:
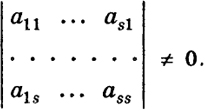
Пусть ранг А = k. Тогда, очевидно, k ≤ п. Существует не равный нулю определитель k-го порядка, порождаемый матрицей А. Не ограничивая общности, можно считать, что это определитель из коэффициентов первых k уравнений системы (2'):
Так как однородная система (10) имеет определитель, отличный от нуля, то она имеет только тривиальное решение: 112 λ1 = λ2 = ... = λk = 0, и система векторов (1) линейно независима. Утверждение теоремы в этом случае доказано. Пусть теперь ранг А = s < k. Перенумеруем переменные λ1 и коэффициенты аij системы (2') так, чтобы
Тогда систему первых s уравнений можно записать так:
Если положить λs+1 = ... = λk = 1, то данную систему можно решить относительно λ1, ..., λs. В результате получим нетривиальное решение λ1, ..., λk (11) первых s уравнений (2'). Теперь мы можем присоединить к этим s уравнениям любые другие k - s уравнений (2'), и полученная система все равно будет иметь найденную нетривиальную систему в качестве решения. Чтобы объяснить это утверждение, запишем формально систему (2') следующим образом:
Матрица из коэффициентов полученных уравнений все равно имеет ранг s, так же как и расширенная (справа нулями!) матрица. Первые s уравнений системы (2') удовлетворяются найденными числами λ1, ..., λk (см. (11)) и произвольными числами λ1, ..., λn. На основании утверждения 2) § 4 (правила 113 решения систем) числа λ1, ..., λп удовлетворяют и остальным уравнениям системы (2'), т. е. числа λ1 ..., λk (не все равные нулю) удовлетворяют остальным уравнениям системы (2'). Таким образом, векторы a1, ..., аk линейно зависимы, и теорема доказана и в этом случае. 114 |
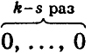 , которая тоже нетривиальна, имело бы место
, которая тоже нетривиальна, имело бы место
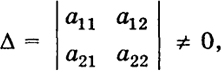


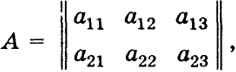
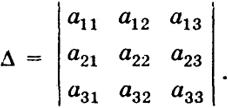
 (7’)
(7’)

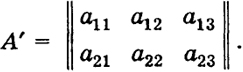 (8)
(8)
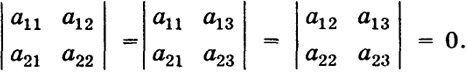

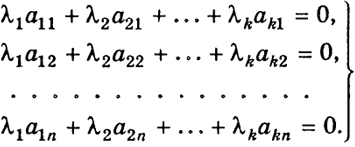 (2')
(2')
 (10)
(10)


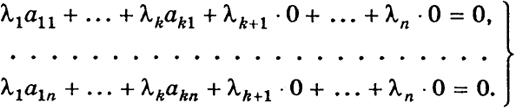 (2')
(2')