| Главная |
Высшая математика. Том 1: Элементы линейной алгебры и аналитической геометрии§ 2. Определители третьего и а-го порядка 2.1. Определители третьего порядка. Число Δ = a11a22a33 + a12a23a31 - a13a22a31 - a11a23a32 - a12a21a33, (1) записываемое в форме
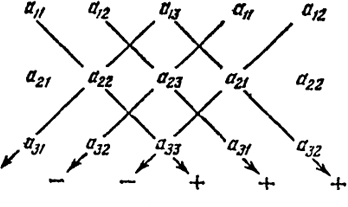
8 где аkl- числа (действительные или комплексные), называется определителем или детерминантом третьего порядка. В определителе (2) различают первую, вторую и третью строки, так же как первый, второй и третий столбцы. Число аklназывается элементом определителя; при этом первый индекс k указывает номер строки, а второй индекс l - номер столбца, к которому принадлежит данный элемент. Будем также говорить, что элемент аklнаходится на пересечении k-й строки и l-го столбца. Элементы определителя а11,.а22, а33 образуют главную диагональ определителя, а элементы а13, a22, a31 - побочную. Можно также говорить, что диагональ, на которой расположены элементы a11, a22, a33 называется главной диагональю определителя (2). Структура выражения (1) довольно проста. Это есть число, вычисляемое по элементам аklпо следующему наглядному правилу (Саррюса): составим таблицу (Саррюса), полученную из элементов определителя (2), если приписать к ним первый и второй столбцы определителя (рис. 1). Мы видим, что надо взять всевозможные произведения элементов, зачеркнутых прямыми; при этом три произведения, соответствующие прямым, параллельным главной диагонали, надо взять со знаком плюс, а остальные три произведения, соответствующие прямым, параллельным побочной диагонали, надо взять со знаком минус.
9 Каждое произведение с указанным знаком называется членом определителя (2). Среди входящих в произведения элементов имеются представители от каждой строки и от каждого столбца. Эти элементы можно в каждом члене расположить в порядке возрастания первого индекса, т. е. номеров строк, к которым они принадлежат. Это и сделано в сумме (1). Что же касается номеров столбцов, к которым принадлежат эти элементы, то их расположения даются ниже:
Это всевозможные перестановки из чисел 1, 2, 3. Перестановку 1, 2, 3 (5) из чисел 1, 2, 3 назовем основной, Говорят, что в перестановке произведена транспозиция двух определенных ее элементов, если эти элементы заменены местами. После транспозиции перестановка переходит в другую перестановку. В этой последней можно сделать в свою очередь транспозицию, в результате получится третья перестановка (но не исключено, что и первая). Например, перестановка 3, 2, 1 (6) получена транспозицией первого и третьего элементов перестановки (5), а перестановка 10 2, 3, 1 (7) транспозицией первого и второго элементов перестановки (6). Важно отметить, что, если некоторая перестановка получена из основной посредством N транспозиций и если эта же перестановка получена из основной каким-либо другим путем посредством N1транспозиций, то оба числа N и N1одновременно либо четные, либо нечетные. Перестановка чисел 1, 2, 3 называется четной (нечетной), если она получается из основной перестановки при помощи четного (нечетного) числа транспозиций. Пусть дана перестановка j = (j1 j2, j3) гДе j1 j2 j3 это числа 1, 2, 3, взятые в некотором порядке. Число транспозиций, с помощью которых можно получить эту перестановку из основной перестановки, обозначим через t(j). Тогда перестановка / является четной (нечетной), если t(j) - четное (нечетное) число. Перестановки (3) - четные, а (4) - нечетные. После сказанного можно дать другое эквивалентное определение определителя 3-го порядка. Определителем или детерминантом 3-го порядка (2) называется число А, равное сумме
произведений вида (-1) t(j) a1j1a2 J 2a3 J 3, где j = (j1, j2, j3) - всевозможные различные перестановки основной перестановки 1, 2, 3. Это определение обобщается на определители или детерминанты n-го порядка (п = 1, 2, 3,...). 2.2. Определители n-го порядка. Определителем или детерминантом n-го порядка называется число, записываемое в виде 11
и вычисляемое по данным числам aik(действительным или комплексным) - элементам определителя - по следующему закону: А есть сумма 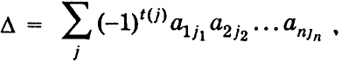 распространенная на всевозможные различные перестановки j = (j1, ..., jn) из чисел 1, 2, ..., n. Число t(j) равно числу транспозиций, которые нужно сделать, чтобы перейти от основной перестановки 1, 2, ..., п к перестановке j - (j1,..., jn). Произведение (-l) t(j) a lj1oooanjnназывается членом определителя. Определители n-го порядка удовлетворяют свойствам а), б), в), г), д), перечисленным в предыдущем параграфе. Доказательство, а) После замены у определителя соответствующих строк столбцами теперь уже номера строк будут обозначаться вторыми индексами. Например, для определителя третьего порядка (2) будем иметь В общем случае общий член нового определителя запишется (-1) t(j) a j11a j22…ajnn 12 Упорядочим множители произведения a j11a j22…ajnn по первому индексу, т. е. мы переходим от перестановки j = (j1,…, jn) к основной перестановке 1, 2, ..., п. При этом мы должны совершить t(j) транспозиций. Тогда основная перестановка вторых индексов перейдет в некоторую перестановку i = (i1..., in) и число t(i) будет той же четности, что и число t(j). Таким образом, (-1) t(j) a j11 … ajnn = (-1) t(i) a1i1 a2i2 … anin Нетрудно видеть, что разным перестановкам j1, ..., jnсоответствуют разные перестановки i1 ..., in. Но тогда 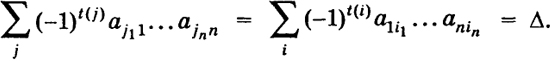 б) Поменяем местами, например, первую и третью строки определителя третьего порядка (2). Тогда получим определитель, который обозначим через Δ', он будет равен 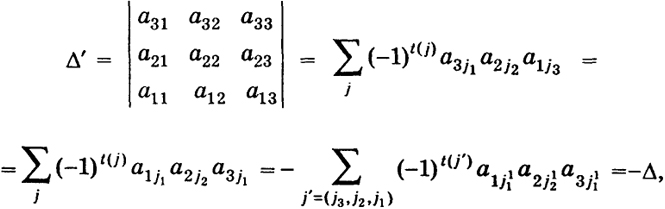 так как перестановка j = (j1 j2, j3) отличается от перестановки j' = (j3, j2, j1) = (j11, j21, j31) одной транспозицией. Будем говорить, что число k умножается на строку (столбец) определителя, если на самом деле k умножается на все элементы строки (столбца). в) Умножение на число k какой-либо строки (столбца) определителя сводится к умножению всех его членов на k, потому что каждый член содержит один элемент указанной строки (столбца). Но тогда величина суммы членов умножится на k. 13 г) Определитель, у которого элементы какого-либо столбца или строки равны нулю, равен нулю, потому что все его члены, очевидно, равны нулю. д) Определитель равен нулю, если он имеет две одинаковые строки или два одинаковых столбца. Это следует из свойства б) (Δ' = -Δ, Δ' = Δ, откуда Δ = 0). Вычеркнем из определителя (9) n-го порядка i-ю строку и k-й столбец. Оставшееся выражение порождает определитель (п - 1)-го порядка М ik, называемый минором элемента aik. Величина же Aik= (-l)i+k Mik называется алгебраическим дополнением или адъюнктом элемента aik. Свойство е) Сумма произведений элементов aik некоторой строки (столбца) определителя на алгебраические дополнения этих элементов равна величине определителя: 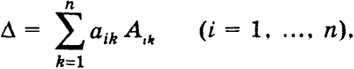 (10) (10)
 (10') (10')
Докажем это свойство для определителя третьего порядка в случае третьей строки. Имеем 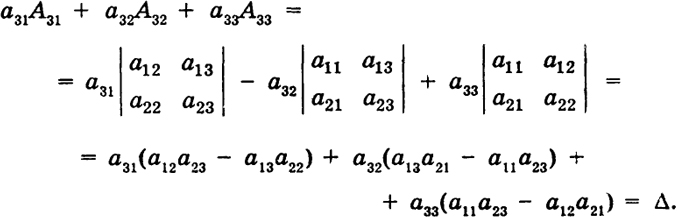 14 Сумму (10) называют разложением определителя по элементам 1-й строки, а сумму (10') - разложением определителя по элементам k-го столбца. Пример 1. Если в определителе Δ (см. (9)) а21 = а31 = = ... = a n1= 0, то Δ = a11А11, т. е. вычисление этого определителя сводится к вычислению одного его адъюнкта, т. е. определителя (п - 1)-го порядка. Пример 2. Если все элементы Д, стоящие ниже (выше) главной диагонали Д, равны нулю (аkl = 0, если k > l (k < l)), то Δ = а11а22 ooo аnn. Это следует из предыдущего примера. Свойство ж) Сумма произведений элементов aik некоторой строки (столбца) определителя на соответствующие адъюнкты элементов другой строки (столбца) равна нулю:
(i ≠ j; i, j = 1, ..., п). В самом деле, зафиксируем наше внимание на первой сумме. Эта сумма не зависит от элементов у'-й строки. Заменим в нашем определителе элементы у'-й строки на соответствующие элементы i-й строки. От этого рассматриваемая сумма не изменится. Между тем теперь ее можно рассматривать как разложение нового определителя по элементам у'-й строки, но тогда она равна величине нового определителя. Но последний равен нулю на основании свойства д), потому что он имеет одинаковые строки - i -ю и j -ю. 15 Свойство з) Пусть даны два определителя n-го порядка Д, и Д2, у которых все строки (столбцы) одинаковы, кроме определенной одной (одного}. Сумма таких определителей равна определителю А n-го порядка, у которого указанная строка (столбец) состоит из сумм соответствующих элементов этой строки (столбца) определителей Δ iи Δ2. Например,  В самом деле, разлагая данные определители по элементам п-го столбца, получим 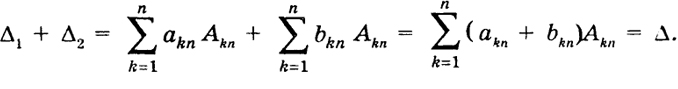 Свойство и) Величина определителя не изменится, если к элементам какой-либо его строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на число k. Например: 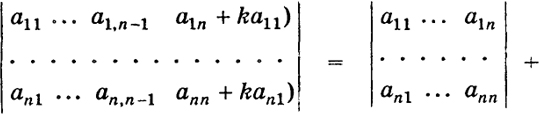 16 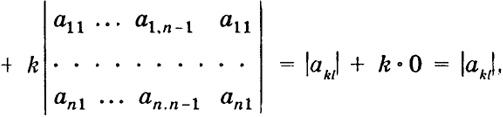 в силу свойств з), в), д). Надлежащее применение этого свойства приводит вычисление данного определителя к вычислению определителя более низкого порядка. Пример 3. 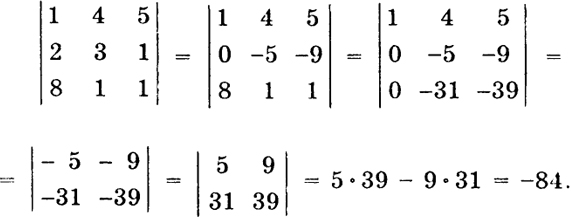 Пример 4.  Пример 5. Определитель  17 порожденный числами а1 а2,..., апназывается степенным или определителем Вандермонда 1. Этот определитель равен нулю, если какие-либо два числа аj и akравны между собой. Если все аjразличны, то
В самом деле, при n= 2 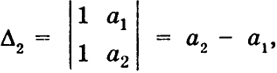 т. е. формула (12) верна. Допустим, что формула (12) верна при п = k - 1, и докажем, что она верна при п = k. Будем использовать свойства и), в) определителя. Умножим k- 1-й столбец в определителе Δk на a1 и вычтем из k-ro, k-2-й столбец умножим также на а, и вычтем из k-1-го и т. д.; тогда получим 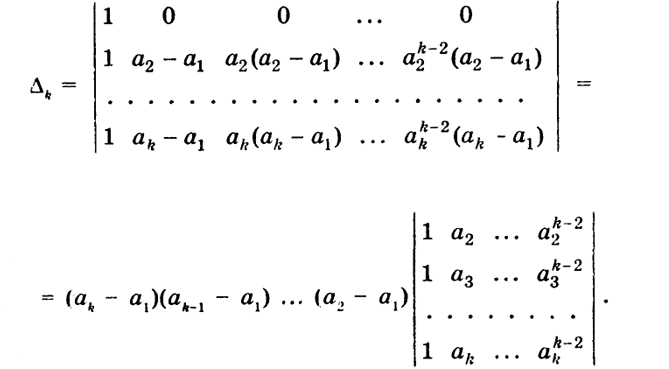 18 Последний определитель есть также определитель Вандермонда порядка (k -1), порожденный числами а2, ..., ak, поэтому, по предположению, имеем 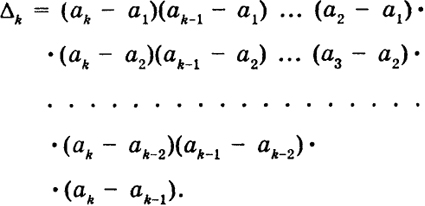 Таким образом, в силу метода математической индукции формула (12) верна при любом п ≥ 2. Свойство к) Пусть Δ1 = |bkl|, Δ2 = |akl| Произведение двух определителей n-го порядка с элементами bkl, аkl есть в свою очередь определитель n-го порядка с элементами 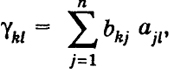 т. е. 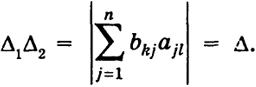 Таким образом, элемент γ kl, принадлежащий к k -й строке и l -му столбцу определителя Δ, равен, как говорят, произведению k -й строки определителя Δ t на l -й столбец определителя Δ2. На самом деле это есть сумма произведений элементов k -й строки определителя Δ1 на соответствующие элементы l -го столбца определителя Δ2. 19 Так как в определителях Δ1 и Δ2 можно менять строки со столбцами, то, очевидно, элементы γ klпроизведения Δ можно строить также, беря произведение k -й строки Δ1 на l -ю строку Δ2 или произведение k -го столбца Δ i. на l -и столбец Δ2 или k -го столбца на 1-ю строку. Доказательство. Убедимся в справедливости свойства на примере определителей второго порядка: 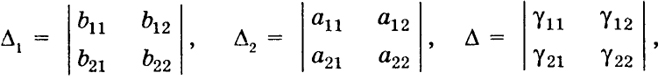 где
γ11 = b11a11 + b12a12, γ12 = b11a12 + b12a22, В силу свойств з), в), д) 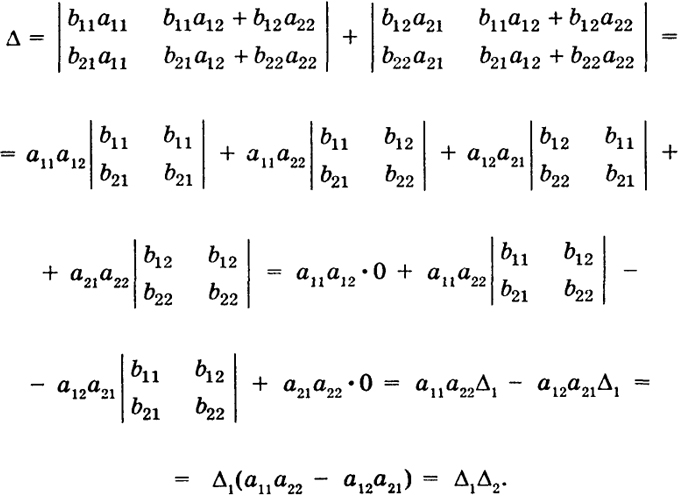 В общем случае определителей n-го порядка можно записать: 20 
При вычислении отдельных элементов Δ мы вправе выбирать любой индекс суммирования 21 системе (s1, s2, ..., sn) две компоненты sITALICи sjравны между собой(sITALIC = sj, i ≠ j), то определитель |bskl| = 0. Поэтому на самом деле в кратной сумме можно оставить только члены, соответствующие разным перестановкам (s1 ..., sn) и натуральных чисел (1, ..., n). При этом, очевидно, окажется, что определитель | bskl | = (-1) t(s) Δ1 22 1 А. Т. Вандермонд (1735-1796) - французский математик. |
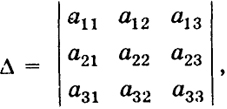 (2)
(2)
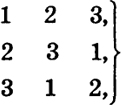 (3)
(3)
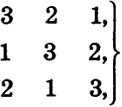 (4)
(4)
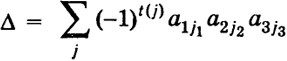 (8)
(8)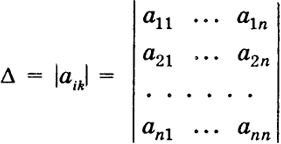 (9)
(9)
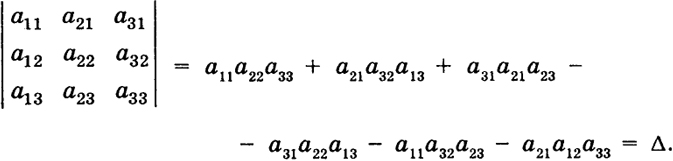
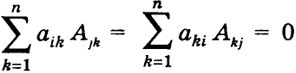 (11)
(11)
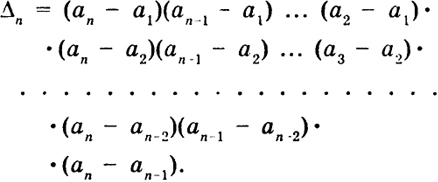 (12)
(12)
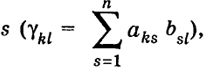 но для дальнейшего удобно для первой строки Δ взять в качестве такого индекс s 1, для второй - s2 и т. д. Второе равенство имеет место на основании свойств з) и в); при этом кратная сумма
но для дальнейшего удобно для первой строки Δ взять в качестве такого индекс s 1, для второй - s2 и т. д. Второе равенство имеет место на основании свойств з) и в); при этом кратная сумма 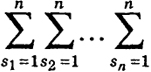 распространяется на всевозможные перестановки(s1, s2, ..., sn), где 1 ≤ s1≤ п. Однако если в какой-либо
распространяется на всевозможные перестановки(s1, s2, ..., sn), где 1 ≤ s1≤ п. Однако если в какой-либо